Virtual Memory Mechanisms
As we can see in the previous post, all allocation algorithms we discussed lead to external fragmentation. As time goes by, external fragmentation is going to get worse and we need solutions for the problem. We can use swap areas to swap out memory onto the disk, or move allocated memory together(a process named memory compaction), leaving empty spaces together. Even these approaches can reduce external fragmentation and allow a higher degree of multiprogramming, they are not perfect. In addition, it is possible to have a single process that is just too big to fit into memory. We are going to discuss methods used to completely eliminate external fragmentation. More than that, we will discuss how to make memory sharing possible and how to allow more processes to execute at once.
Too big to fit
It’s easy for us to assume the amount of available memory that can be allocated is not a big problem. It’s easy for programmers to assume the available memory resource is almost infinite and thus we rarely care about the situation in which the code we wrote is going to occupy all memory resource. But let’s just consider the scenario where we create a program which later create a process that is just too big to fit into memory, what should we do?
The natural response would be: just cut them into pieces! This is a technique called overlay: programmers manually cut the program into pieces, or overlays. When the program executes, a overlay manager is created to swap pieces in and out, allowing only necessary pieces in memory at a given time. But tell me, what is the last time you see an user-level application manually cut into “pieces” by the programmer? Doing things manually is not desired trait of a programmer. Programmers should always be lazy and automate things, or just leave it to someone else!
Paging
I’m pretty sure you don’t like the idea of overlaying as it requires you to do things manually. That’s where paging comes into play. Instead of dividing the program by the programmer, why don’t we let the system do the dirty job? Before we start, I’m going to throw two questions to you: why can a virtual address space be bigger than the physical memory? How are each piece of a process brought into the memory?
The technique to divide a address space into fixed-size pages is called paging. A copy of the address space is stored on the disk. The physical memory is viewed as a series of equal-sized page frames. We will discuss later about how the system choose to load a page into a frame and how to manage pages that are currently in memory.
So how do we use virtual addresses with the our recently introduced pages to find a location in memory? As we can see, a virtual address space is divided into pages, each with a fixed number of entries. In order to represent the number of pages and number of entries, we need two variables:
p - page number(pMAX pages)
o - page offset (difference between the byte address to search and the start of the page, MAX indicates the total number of entries in a table)
Virtual Address calculation: oMAX x p + o (here o is the offset in the last page)
The frame size is equal to that of a page. It’s easy to understand since we need to put everything stored in a page into the frame, we need them both to be equally sized. Note that since virtual address space can be bigger than physical memory, the number of frames can be smaller than the number of pages, which means the number of bits reserved for frame number can be smaller than the number of bits used to indicate the number of pages.

From Virtual to Physical: Allocation Policy
We’ve discussed how that a process’s virtual address space can be divided into pages and mapped to frames in physical memory. Here we are going to discuss some policies used to implement the mapping process. I’m going to leave three questions to think here as well: why pages are arbitrarily located in physical memory? How do we find them if they are arbitrarily located in physical memory? Why aren’t all pages mapped to frames? These questions will become more clear as we progress into further discussion.
Here’s the solution: a page table. Each process has one page table that contains all mapping information for each possible virtual address belonged to that process. Even though we call it table, it’s merely a data structure used by a virtual memory system in a computer operating system to store the mapping between virtual addresses and physical addresses. However, the mapping is invisible to the process. The protection mechanism is the same as dynamic relocation we’ve discussed before.
Virtual Address Translation
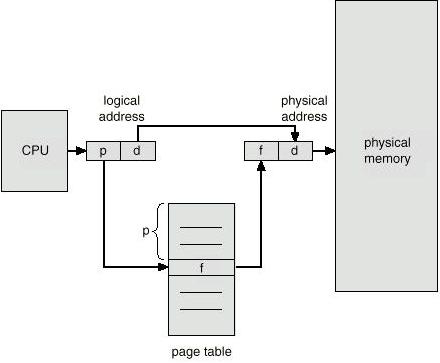
Now we are going through a step-by-step description of address how to translate virtual address to physical address.
First, the process will give the CPU a virtual address to translate.
Then MMU will split the address into two parts, the page number and the offset.
Since the size of a page and a frame are the same, the offset of the virtual address is sent along without no modification to the physical memory.
Use page number to find the corresponding entry in the page table.
Check if the page exists in physical memory.
If the page does exist in physical memory, the frame number is sent along. If the requested page is on the disk, then the corresponding page is moved to memory and frame number is recorded now.
Offset is appended to the end of the frame number to get the physical address.
So, we’ve achieved several goals now by using paging technique:
Reduce or even eliminate external fragmentation.
Easy to grow processes.
Allow more process that is too big to fit into memory to be able to execute.
Easy to allocate and deallocate.
Share memory is between processes is easy since memory used by difference processes no longer has to be contiguous. Even pages may exist in different position, they can be mapped to the same physical address in memory.
More about Page Table
One thing to notice is that there’s only one page table for each process. The page table is part of the process’s state and serves as protection mechanism to prevent processes accessing each other’s memory. There’re several elements in each page table entry as well:
Flags: dirty bit, resident bit, and dirty bit (we will talk about them later). Flag is stored at the beginning of each entry.
Frame number: stored in the remaining bits. It tells where the page lives in physical memory.
However, page table still has its disadvantages, the most important thing to notice is that we need two memory accesses to implement virtual memory reference, first access is to get the page table entry, the second access is used to get the actual data from memory, if it’s present. As we know, memory access is extremely slow and expensive, thus we need something faster.
Translation Look-aside Buffer (TLB)
Since it’s hard to improve the speed from the algorithm side, let’s just drop the algorithm for a minute and switch our focus onto the hardware. Here we will discuss how to improve the speed of memory reference by adding a hardware component called TLB. Here are several basic characteristics of TLB:
The TLB holds recently used frame/page pairings.
It has high hit ratios due to locality.
For a TLB hit, translation can be finished in one cycle.
So how does TLB help with efficiency? It’s actually really simple. The system simultaneously sends the page number to both page table and TLB. If there’s TLB hit, then the TLB cache sends the frame number to the memory without having to look into the page table, which avoids the first reference into the memory to find the page table. If there’s missing TLB, everything stays the same: look for the page table in memory and update the TLB.

Problems with Page Table
Now we solved the problems of external fragmentation. It seems paging works like a charm and makes things a lot easier. However, we notice it’s still not perfect in terms of space usage:
Data structure overhead (The page table can be huge!)
Inappropriate page size can lead to internal fragmentation, and less processes to exist in memory in the same(page too big)!
Thus we need more complex methods to solve the above issues.
Multi-level Page Tables
The basic concept of multi-level page table is to subdivide page number into n parts(n stands for number levels of pages tables). n is decided by the architecture of the system. Each entry in each page table which is exists each entry points to the corresponding page table in the next level. The last level page table entries hold the bit/frame information associated to the page table entry.
SO how does it work exactly? First, we have only one first-level page table. We extract the first subdivision of the virtual address, added to the PTBR to get the corresponding entry in the first-level page table. Then we extract the second subdivision of the virtual address, add it to the address of the beginning of the second-level page table which we got from the corresponding first-level page table entry. This process continues until we reach the last-level page table. From the corresponding entry we can get the frame number. The offset is preserved so we just need to append the offset to the frame number and we’re done! One reminder is that multi-level page table requires several lookups to eventually find the frame number, so TLB becomes extremely important here in terms of improving performance.
How does multi-level page table save space?
You’re probably still confused why multi-level page table saves space by adding more tables. Don’t worry, I will walk you through an example to illustrate the magic behind the scene:)
Assume a process has a ((2^{10}\) pages, each PTE occupying 4 bytes (32-bit system). Without multilevel page table, we need \(2^{20} \times 4 = 4MB\) for one page table stored in memory. Even we just need a portion of all pages, we need the whole page table present in memory to find the corresponding frames. Now, if we divide the virtual address into 3 sections with last one being the offset, we have a two-level page table. The first 10 bits are used to index the page table in the first level and the next 10 bits are used to index the page table in the second level. If we only need virtual addresses that have the second 10 bits modified and leave the first 10 bits untouched, then we only need to find one entry in the first-level page table. Since the first-level page table has to be always present in memory, it will consume \(2^{10} \times 4=4KB\) memory space. Now, since we need every entry in a second-level page table pointed by the entry we just found in an entry in the first-level page table, it requires \(2^{10} \times 4bytes = 4KB\) memory. So we only need to use 4 + 4 = 8KB for all memory we need instead of 4MB without multi-level page tables.
Another interesting fact is that, even if we need to use all pages of a process, multi-level page table will potentially increase the space needed. Let’s take the above example and assume we need every single pages from a process. Then we need to store the first-level page table, which takes $2^{10} \times 4bytes = 4KB$. Then, for each entry in the first-level page table, there’s a corresponding second-level page table, each with the size of \(2^{10} \times 4 = 4KB\). Since the first-level table has \(2^{10}\) entries, the total number of second-level page tables is \(2^{10}\), each with the size of 4KB, so the total amount of spaces is \(2^{10} \times 4kb + 4kb = 4MB + 4KB\). Then bottom line is: if we need to map every pages to its frames, then the total amount of entries in the last level will be the number of pages regardless of how many levels we use since each page has to have a mapping. Under such case, the total amount of memory used by the last-level page tables will be equivalent to the amount used when we use only one huge page table. The additional space comes from the upper levels, but the previous level will only save the corresponding number of entries. (number of table in the next level).
