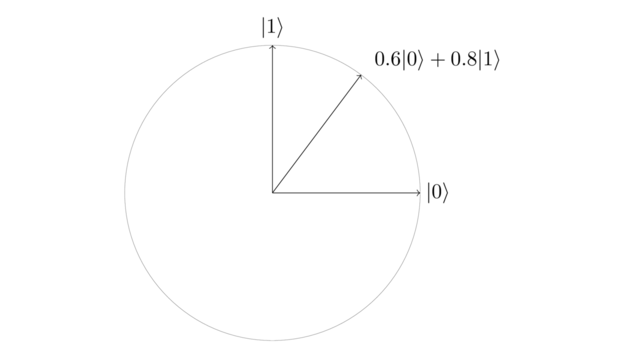Quantum State in a Nutshell

There are thousands of articles trying to explain what exactly a quantum state is. Many of them boiled down to “the state of a qubit is 0, 1, or 0 and 1 at the same time”. This statement leads to both confusion and misinterpretation. The explanation I found on Quantum computing for the very curious is by far the most elegant and simplest:

The state of a qubit is a vector in a two-dimensional vector space. This vector space is known as state space.

I will use many of great content from Quantum computing for the very curious to explain things.

Mapping qubits to classical bits

We’ve described what a qubit state is, but provided no link between a qubit state and a classical bit state. There are two possible states for a classical bit: 0 and 1. The corresponding states for a qubit is slightly fancier: \(|0\rangle \) and \(|1\rangle \).

The notation with \(|\) and \(\rangle\) is called a \(ket\) notation. With a number wrapped between them, \(0\) or \(1\) are called \(kets\). A \(ket\) is a fancy term for a vector. In fact, \(|0\rangle\) is really just \( \begin{bmatrix} 1 \newline 0 \end{bmatrix} \); \(|1\rangle\) is really just \( \begin{bmatrix} 0 \newline 1 \end{bmatrix} \).

States between 0 and 1

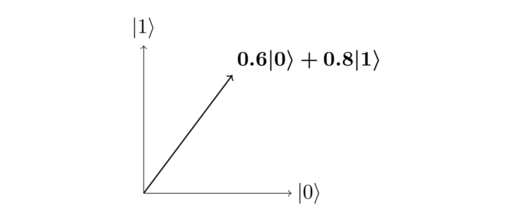
Both the states \(|0\rangle\) and \(|1\rangle\) are called computational basis states, which maps to classical 0 and 1 states. There are more states for a qubit. We’ve already learned that a quantum state is a two-dimensional vector. An example is given:

The state \(0.6|0\rangle + 0.8|1\rangle\) is just a combination of the \(|0\rangle\) vector and the \(|1\rangle\) vector. A state like this is a superposition of \(|0\rangle\) and \(|1\rangle\), a fancy way of saying a linear combination of \(|0\rangle\) and \(|1\rangle\). \(0.6\) is the amplitude for state \(|0\rangle\), and \(0.8\) is the amplitude for state \(|1\rangle\).

Not all linear combination of vector \(|0\rangle\) and \(|1\rangle\) are qubit states. There is one constraint: the sums of the squares of the amplitudes must be 1. For example, we can compute \(0.6^2 + 0.8^2\) and verify the result is 1.

For general quantum states, the amplitudes can be complex numbers as well. Denoting both amplitudes as \(\alpha\) and \(\beta\), a quantum state can be formally written as:

\[\alpha |0\rangle + \beta |1\rangle \wedge \alpha^2 + \beta^2 = 1\]

\(\alpha^2 + \beta^2 = 1\) is called the normalization constraint.

If we think of \(|0\rangle\) and \(|1\rangle\) as orthonormal vectors, we can visualize the possible linear combination of these two vectors as a circle of radius 1:

Since amplitudes can be complex numbers, the state space really becomes a sphere. Summing all these up:

the quantum state of a qubit is a vector of unit length in a two-dimensional complex vector space known as state space.

– Quantum computing for the very curious

Measuring a qubit

Suppose we have qubit in a quantum state \(\alpha |0\rangle + \beta |1\rangle\). We want to observe the state of this specific qubit. It turns out the law of physics prohibits us from figuring out the the amplitudes \(\alpha\) and \(\beta\) if they start out unknown. In short, the quantum state of any system is not directly observable.

To figure out the quantum state. We rely on a process called measurement in the computational basis. Suppose a qubit is in the state \(\alpha |0\rangle + \beta |1\rangle\). Measuring the state of this qubit gives us the outcome \(0\) with probability \(|\alpha|^2\), or 1 with probability \(|\beta|^2\). The state of the qubit after the measurement is thus either \(|0\rangle\) or \(|1\rangle\). After the measurement, \(\alpha\) and \(\beta\) are gone.