Maximum Likelihood for Classification

Let’s say we want to classify an input text \(y\) and give it a label \(x\). Formally, we want to find:

\[ \textrm{argmax} P(x | y) \]

By Bayes’ rule this is the same as

\[ \textrm{argmax} \frac{P(y|x)P(y)}{P(x)} \]

Suppose we have five documents as training data and one document as the input as testing data. Our objective is to give a label to the test sentence.

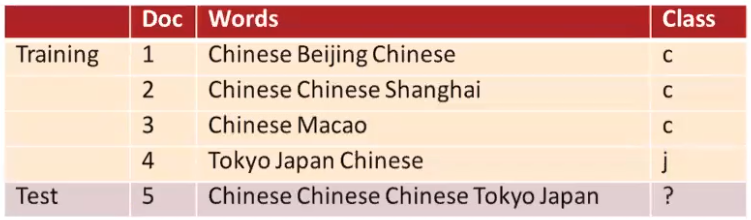
Let’s define the probability of class as (\(N\) is the total number of classes)

\[ p(x) = \frac{count(x)}{N} \]

and the probability of a word appearing given a class label (total number of vocabs)

\[ p(w_i|x) = \frac{count(w_i,x) + 1}{count(x) + |V|} \]

The conditional probabilities for \(p(w_i|y)\) is

Now, we want to find out which language label should we assign the sentence “Chinese Chinese Chinese Tokyo Japan”. This is the same as asking which labels (\(x\))) should we pick so that \(P(W|x)P(x)\) yields the greatest value. Mathematically, we want to find out where the gradient of the function \(P(W|x)P(x)\) is flat.

If we label the sentence as j (Japanese), we have \(P(j | d_5) \propto \frac{1}{4}\cdot (\frac{2}{9}^3)\cdot \frac{2}{9}\cdot \frac{2}{9} \approx 0.0001\). If we calculate \(P(c|d_5)\), we get 0.0003, which generates the largest value for \(P(x | y)\).