Lamport Distributed Mutual Exclusion
Normally, having consistent event ordering in a distributed system is hard because we have no common clock. Since we don’t have a common clock to measure with, we rely on logical properties of time in the absence of clock. Here we use causality replation between events.
In essence, Causality indicates a clock \(C\) is map from events to time satisfying: \(e\rightarrow e’\) implies \(C(e) < C(e’)\)
We can synthesize a clock by a simple protocol, usually referred as scalar clock or Lamport clock:
- Each process \(p\) has a local clock \(C(p)\).
- A message send by a process is stampled with the its corresponding local clock.
- On receiving \(M\), set the process’s local clock to be \(max(C(p), C(M)) + 1\).
This will give us a consistent total order of events in a distributed system.
Let’s take Lamport distributed mutual exclusion (DME) as an example. We use scalar clock to agree on the order of access to critical sections. Each process broadcasts a request with its local clock time. Receiver stores the request time and responds with its update local time (\(max(C(p), C(M)) + 1\)).
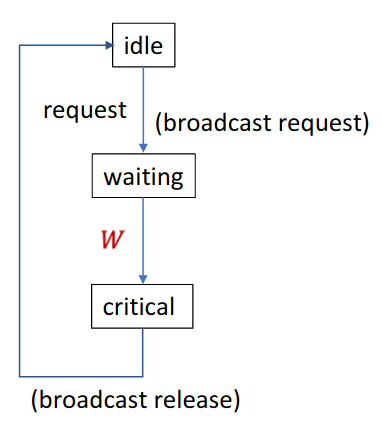
A process can only enter critical section given the condition \(W\) is met: \(W \equiv \forall q \neq p,\ t(p,q) > r(p,p) \land r(p,p) < r(p,q)\). \(t(p, q)\) represents the latest time received by \(p\) from \(q\). \(r(p, q)\) is the request time received by \(p\) from \(q\) or \(+\infty\). Intuitively, it says if a process’s request time is smaller than all repsonses time and the process’s request time is smaller than all the other request time, then this process is the first one to send out the request and thus should enter critical section.
The reason why this protocol works is illustrated below:
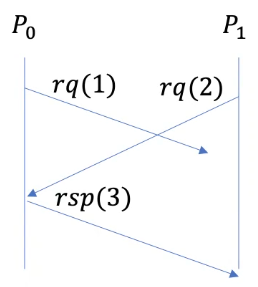
When \(p_1\) sends a request at timestamp 2 and gets a repsonse with timestamp 3, we know \(p_1\) has the greatest clock value and \(p_0\) will update its own clock based on the timestamp sent from \(p_1\). Now \(p_1\) sees the response message from \(p_0\) with timestamp 3, it knows any request from \(p_0\) must have already been received, because the network channel is ordered and any request sent by \(p_0\) already arrived before the response with timestamp 3.
To see Lamport DME in action, we use Ivy to specify the protocol. The source file is borrowed from Ken’s presentation. The code is annotated and self-explanatory:
#lang ivy1.8
# This is an implememtation of Lamport's distributed mutual excluson
# (DME) algorithm.
include order
include network
# We start the module with a 'global' section. This contaions the
# declarations of any resources that are used in common by all
# processes. These usually include:
#
# - Data types
# - Services, such as network services
# - Immutable global parameters, such as netwrok addresses
#
# We can't have mutable global variables, since processes, being
# distributed, don't have shared memory.
#
global {
# Our first global data type is the type of host identifiers. We
# will have one process for each value of this type. Host
# identifiers take on integer values from `0` to `node_max`.
# We create the host identifier type by instantiating the
# `host_iterable` module. It has a parameter `max` that gives the
# maximum value of the type (and is supplied at run time).
instance host_id : iterable
# Since we have three kinds of messages in our protocol, we define
# an enumerated type for the message kind with three symbolic
# values.
type msg_kind = {request_kind,reply_kind,release_kind}
# In addition, we use a sequence type to represent timestamps. The
# `unbounded_sequence` template in the `order` library gives a
# discrete totally ordered type with a least value `0` and a
# `next` operator.
instance timestamp : unbounded_sequence
# Our messages are stucts with three fields: the message kind and the
# host identifier of the sender and a timestamp. We order messages
# according to the timestamp. This ordering is useful in the proof
# of correctness.
class msg_t = {
field kind : msg_kind
field sender_id : host_id
field ts : timestamp
# definition (M1:msg_t < M2:msg_t) = ts(M1) < ts(M2)
}
# A useful enumerated type to describe node state:
type state_t = {idle,waiting,critical}
# Finally we instantiate a network service via which our processes
# will communicate. Here, `transport.net` is a template defined in the
# `network` library that we included above. The template takes one
# parameter, which is the type of messages to be sent. Our instance
# of this template is an object called `net`.
instance net : tcp.net(msg_t)
}
# After the global section, we introduce some distribtued processes.
# A process with parameters has one instance for each value of the
# parameters. In this case we have one parameter of type `host_id`
# which means there is one process in the system for each value of
# `host_id` in the range `0..host_id.max`. The parameter is named `self`.
# This means that the process can refer to its own host identifier by
# the name `self`.
process node(self:host_id) = {
# A process usually begins by declaring an *interface*. This
# consists of a set of *actions* that are either calls in from the
# environment (exports) or calls out to the environment (imports).
# Our action is an export `request`, which our client uses to
# request to enter the critical section. It takes no parameters.
export action request
# Our second action is an import `grant`. This is a callback to
# the client indicating that is is safe to enter the critical
# section.
import action grant
# Our third action is an export `release`. This is called by the
# client when exiting the critical section, indicating it is safe to
# another process to enter.
export action release
common {
specification {
var client_state(H:host_id) : state_t
after init {
client_state(H) := idle;
}
before request(self:host_id) {
require client_state(self) = idle;
client_state(self) := waiting;
}
before grant(self:host_id) {
require client_state(self) = waiting;
require client_state(X) ~= critical;
client_state(self) := critical;
}
before release(self:host_id) {
require client_state(self) = critical;
client_state(self) := idle;
}
}
}
implementation {
# Next we declare per-process objects. Each process needs a socket
# on network `net` in order to communicate. We declare the socket
# here. The socket `sock` is an instance of the template `socket`
# declared by the network service `net`.
instance sock : net.socket
# We also declare some local (per-process) types and variables.
var state : state_t
# We also keep track of the current timestamp
var ts : timestamp
# Each process maintains a 'request queue', which a map from host_ids to
# the timestamp of the current request from that host, or `0` if none.
var request_ts(X:host_id) : timestamp
# This map records the highest timestamp of a reply received from
# each host.
var reply_ts(X:host_id) : timestamp
# Having declared our variables, we initialize them. Code in an
# `after init` section runs on initialization of the process. You
# aren't allowed to do much here, just assign values to local
# variables.
after init {
state := idle;
ts := 0;
request_ts(X) := 0;
reply_ts(X) := 0;
}
# Now we come to the implementation code. Here we implement our
# exported actions, if any, and also any callback actions from the
# services we use (i.e., actions that these services import from
# us).
# We start with the `request` action. This builds a request message,
# appends it to the request queue, and broadcasts it. The action `broadcast` is
# a local action (i.e., a subroutine) and is defined later.
implement request {
ts := ts.next;
var outgoing : msg_t;
outgoing.kind := request_kind;
outgoing.sender_id := self;
outgoing.ts := ts;
broadcast(outgoing);
request_ts(self) := ts;
state := waiting;
# BUG: should check waiting condition here, if host_id.max = 0
}
# Next we implement the callback `recv` from our network socket,
# indicating we have an incoming message. This is called
# `sock.recv`. It gives us as input parameters the network address
# of the sending socket (not useful here) and the incoming
# message.
implement sock.recv(src:tcp.endpoint,incoming:msg_t) {
# debug "recv" with self = self, src = src, msg = incoming;
# First, we update out timestamp to reflect the incoming
# message.
ts := timestamp.max2(incoming.ts,ts).next;
# We partly construct an outgoing message
var outgoing : msg_t;
outgoing.sender_id := self;
outgoing.ts := ts;
# What we do here depends on the kind of message.
# When we receive a `request` message, we put it on our request queue,
# and return a reply message to the sender.
if incoming.kind = request_kind {
outgoing.kind := reply_kind;
request_ts(incoming.sender_id) := incoming.ts;
unicast(outgoing,incoming.sender_id);
}
# When we receive a `release` message, the sender's request
# must be at the head of our queue. We dequeue it.
else if incoming.kind = release_kind {
request_ts(incoming.sender_id) := 0;
}
# On a reply, we update the highest timestamp received from
# this sender. Because of in-order devlivery, the timestamps
# are received in increasing order, so the incoming one must
# be the greatest so far.
else if incoming.kind = reply_kind {
reply_ts(incoming.sender_id) := incoming.ts;
}
# Having proceesed the incoming message, we might now be able
# to enter our critical section. We do this if:
#
# - We are in the waiting state
# - Our request message has the least timestamp in lexicographic order
# - Every host has sent a reply later than our request
# debug "waiting" with self = self, rq = request_ts(X), ts = reply_ts(X);
if state = waiting
& forall X. X ~= self ->
(request_ts(X) = 0 | lexord(request_ts(self),self,request_ts(X),X))
& reply_ts(X) > request_ts(self)
{
state := critical;
grant;
}
}
implement release {
ts := ts.next;
request_ts(self) := 0;
var outgoing : msg_t;
outgoing.sender_id := self;
outgoing.ts := ts;
outgoing.kind := release_kind;
broadcast(outgoing);
state := idle;
}
# At the end, we have definitions of internal (non-interface)
# actions (in other words, subroutines) and functions (i.e., pure
# functions).
# This function takes two timestamp-host_id pairs and determines
# whether (X1,Y1) < (X2,Y2) in lexicogrpahic order.
function lexord(X1:timestamp,Y1:host_id,X2:timestamp,Y2:host_id) =
X1 < X2 | X1 = X2 & Y1 < Y2
# The action `unicast` sends a message to just one process.
# To actually send a mesage to a socket, we call the `send` action
# of our socket, giving it the receiving socket's network address
# and the message to be sent. Notice we can get the network
# address of process with identifier `idx` with the expression
# `node(idx).sock.id`. This might seem odd, as we asre asking for
# the local state of an object in another process. This is allowed
# because the network addresses of the sockets are immutable
# parameters that are determined at initialization and are
# provided to all processes.
action unicast(outgoing:msg_t, dst_id : host_id) = {
# debug "send" with dst = dst_id, msg = outgoing;
sock.send(node(dst_id).sock.id,outgoing);
}
# Action `broadcast` sends a message to all processes with
# identifiers not equal to `self`. We use a 'for' loop to
# iterate over the type `host_id`. The 'for' construct defines
# two variables:
#
# - `it` is an 'iterator' of type `host.iter`
# - `dst_id` is the value of the type the iterator refers to
#
# The reason we do it this way is the the finite subrange type
# `host_id` has no value the is 'past the end' of the type, so
# you can't write a traditional 'for' loop over this type. The
# iterator type, however, does have a value corresponding to
# 'past the end'.
action broadcast(outgoing:msg_t) = {
for it,dst_id in host_id.iter {
# do not send to self!
if dst_id ~= self {
unicast(outgoing, dst_id);
}
}
}
}
}
# To compile and run with 3 nodes:
#
# $ ivyc lamport_mutex.ivy
# $ ivy_launch host_id.max=3
#
# To test:
#
# $ ivyc target=test lamport_mutex.ivy
# $ ivy_launch host_id.max=3
#
# Bounded model checking:
#
# TODO: As usual, we need the assumption that all endpoint id's are
# distinct.
axiom node(X).sock.id = node(Y).sock.id -> X = Y
# This says to try bounded model checking up to 20 steps (but Ivy
# won't actually get that far). The second parameter say to unroll the
# loops three times. This means that BMC ignores all executions in
# which a loop is executed more than three times. We need this because of
# the loop in `node.broadcast`
attribute method = bmc[20][3]
# Try adding a bug and see if you can find it with testing and bmc. Change
# this definition above:
#
# function lexord(X1:timestamp,Y1:host_id,X2:timestamp,Y2:host_id) =
# X1 < X2 | X1 = X2 & Y1 < Y2
#
# to this:
#
# function lexord(X1:timestamp,Y1:host_id,X2:timestamp,Y2:host_id) =
# X1 <= X2 | X1 = X2 & Y1 < Y2
#
# This mistake could allow two nodes with requests with the same timestamp
# to enter the CS at the same time. Here's a counter-example produced
# by BMC (it takes a while!):
#
# > node.request(1)
# > node.request(0)
# > node.sock.recv(0,{tcp.endpoint.addr:...,tcp.endpoint.port:...},{msg_t.kind:request,msg_t.sender_id:1,msg_t.ts:1})
# > node.sock.recv(1,{tcp.endpoint.addr:...,tcp.endpoint.port:...},{msg_t.kind:request,msg_t.sender_id:0,msg_t.ts:1})
# > node.sock.recv(1,{tcp.endpoint.addr:...,tcp.endpoint.port:...},{msg_t.kind:reply,msg_t.sender_id:0,msg_t.ts:2})
# < node.enter_cs(1)
# > node.sock.recv(0,{tcp.endpoint.addr:...,tcp.endpoint.port:...},{msg_t.kind:reply,msg_t.sender_id:1,msg_t.ts:2})
# < node.enter_cs(0)
# lamport_mutex_save.ivy: line 137: error: assertion failed