Consistency Models Explained
In a distributed system, eventual consistency provides a weak guarantee that data updates will be reflected in all nodes eventually. However, the downside of eventual consistency is that clients could potentially observe awkward intermediate states. For example, appending numbers to a client may result in states like [10], [10,13], [10,12,13].
Therefore, we need stronger consistency guarantees, which is easier to reason about. These consistency models provide various degree of consistency guarantees. However, it’s not always feasible to provide the strongest consistency guarantee. Usually, one needs to trade off consistency for availability and partition resilience (CAP theorem). Many contents here are attributed to Prof. Ken McMillan.
Global Consistency
The most primitive notion of consistency is global consistency. It means we have some history of events that is totally ordered.
It is (globally) consistency if it respects the intended sequential semantics of the events.
– Kenneth McMillan
Take read/write as an example, we have a sequence of write operations to the same memory location \(12\) at various timestamps, and we want to read values from the this location:
\[ \texttt{write}(0, 12, 2) \rightarrow \texttt{write}(1, 12, 3) \rightarrow \texttt{read}(2, 12, 3) \]
If we have global consistency, every read at a given memory location \(x\) will yield the most recently written value to \(x\).
In reality, it’s impossible to implement a global clock in a distributed system. Therefore, no node can observe the entire history of ordered events, making global consistency hard to implement.
Linearizability
In essence, linearizability is an approximation of global consistency. The difference is linearizability is based on logical time, as opposed to physical time used in global consistency. It means we don’t care in what order the event occur physically. We just want the ordering of events to be consistent to what we know about time, and what we know about time is based on causality.
Linearizability has two assumptions:
- Clients don’t have shared clock, but are able to send messages to each other. In other words, we want to create an illusion of global consistency by causality.
- If an event \(e_1\) ends before another event \(e_2\) begins in physical time, then \(e_1\) happens-before \(e_2\). We define the happen before relationship as \(hb(e_1, e_2)\). In simpler terms, is it possible for us to assume a causal connection between two events?
Take the following scenario as an example. We can say \(hb(e_1, e_2)\) holds because we can establish a causality relation between these two events. We are able to assume \(P_1\) sent a message \(m_1\) to \(P_2\), which caused the execution of \(e_2\).

Here is another example. Here, we can not establish a causal connection between \(e_1\) and \(e_2\) because we can not assume \(m_1\) caused the execution of \(e_2\)

To say a set of events, denoted as \(E\), is linearizable, the following conditions must be met:
- There exists a total order \(<_{lin}\) over events \(E\) s.t.
- \((E,\ <_{lin})\) is globally consistent.
- \(hb(e_1, e_2) \rightarrow e_1 <_{lin} e_2\)
In other words, a set of event \(E\) is linearizable if it respects the happen-before relationship, and is totally ordered.
Let’s look at one example. Suppose we have two processes \(P_1\) and \(P_2\). \(P_1\) writes 1 to location 0, and later reads from 0 and gets 1. \(P_2\) writes 2 to location 0 before \(P_1\) finishes its write.
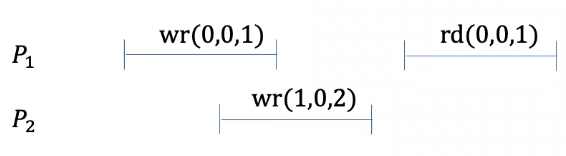
These events are linearizable. We can order these three events as:
\[ \texttt{write}(1, 0, 2) \rightarrow \texttt{write}(0, 0, 1) \rightarrow \texttt{read}(0, 0, 1) \]
We know \(\texttt{write}(0, 0, 1)\) happens before \(\texttt{read}(0, 0, 1)\). The read gets the most recently written (not physical time, but causality) value, satisfying global consistency. Therefore, these events are linearizable.
Here is another example showing events that are not linearizable.

No matter how you order these four events, there will always be a contradiction. For example, \(rd(0,0,1)\) happens after \(wr(1,0,2)\) and \(wr(0,0,1)\). In order to satisfy global consistency requirement (reading the most recently written value), we must order these three events as
\[ wr(1,0,2) \rightarrow wr(0,0,1)\rightarrow rd(0,0,1)\rightarrow\ ? \]
However, \(wr(0,0,1)\) happens before \(rd(1,0,2)\), so \(rd(1,0,2)\) must be put after \(wr(0,0,1)\), but that way the most recently written value would be 1 and it would be impossible to read value 2, thus violating global consistency.
Commit Points
A different and perhaps easier way of thinking linearizability is using commit points. We say a set of events \(E\) is linearizable if every event can be assigned a physical commit time \(t_e\) such that:
- \(t_e\) occurs during the execution of an event \(e\).
- \((E,\lt _{lin})\) is globally consistent, where \(e < _{lin}\ d\) iff \(t_e < t_d\)
The following picture presents a scenario where we set three commit points on three write/read operations.
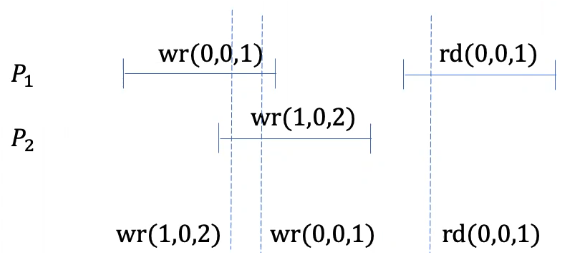
We know these events are linearizable because the three commit points we picked respects the \(\lt_{\textrm{lin}}\) relationship. The commit point \(wr(0,0,1)\) is set after the commit point for \(wr(1,0,2)\) and we know \(wr(1,0,2)< _{lin}wr(0,0,1)\).
Sequential Consistency
We can relax the requirement of linearizability even more, which leads us to sequential consistency. Sequential consistency (Lamport) is based on slightly different assumptions compared to linearizability:
- Assume clients don’t send messages to each other
- \(hb _{sc}(e_1, e_2)\) only holds if \(e _1\) executed before \(e _2\) in the same process.
These assumptions indicates each process doesn’t know the relative order of operations happening on other processes. Thus, we don’t have happen-before arc between processes.
Take the following example:
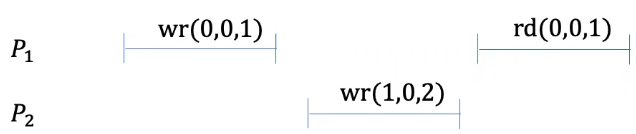
We know these events meets sequential consistency by the following order. The reason is that we can’t say \(hb_{sc}(wr(0,0,1), wr(1, 0, 2))\) must hold. This example would not be linearizable because \(wr(0,0,1)\) happens before \(wr(1,0,2)\).
\[ wr(1, 0, 2) \rightarrow wr(0,0,1) \rightarrow rd(0,0,1) \]
Take another example that is not sequentially consistent:

For \(rd(0,0,2)\) to be true, it must be that \(hb_{sc}(wr(0,0,1), wr(1,0,2))\) holds; for \(rd(1,0,1)\) to be true, iut must be that \(hb_{sc}(wr(1,0,2), wr(0,0,1))\) holds. Now we have a circle of ordering constraint, thus reaching a contradiction.
Causal Consistency
Causal consistency is an even weaker consistency model compared to sequential consistency. However, unlike all the consistency models we discussed before, causal consistency only applies to read/write operations. In causal consistency model, we define a causal order on those read/write operations such that read operations must see writes in order that respects causality.
Precisely, we define a reads-from map, denoted as \(RF\). \(RF\) of a read event \(e\) is going to produce the write operation that gave me the read value (there will be ambiguity if there are two writes writing the same value). For example, \(RF(rd(1,0,2))\) will produce the value \(2\), which is equal to the value written by a write operation \(wr(0,0,2)\). Putting \(RF\) in formal terms:
\[ RF(rd(p,a,v)) = wr(p’,a’,v’) \rightarrow a=a’ \land v = v' \]
In addition, \(hb_{RF}\) is the least transitive relation such that:
- \(hb_{SC}(e, e’) \rightarrow hb_{RF}(e,e’)\)
- \(RF(e’) = e \rightarrow hb_{RF}(e,e’)\). It means whoever gave me the value must happen before me, which represents a notion of causality.
We say a set of events \(E\) is causally consistent if there exists a \(RF\) map for \(E\) such that:
- For all reads \(e\in E\), there is no write \(e’ \in E\) such that \(hb_{RF}(RF(e),e’)\) and \(hb_{RF}(e’,e)\) have the same address.
In layman’s term, it says that if a write operation \(e\) causes us to read a value \(x\), it can’t be that there is another write operation \(e’\) that happens after \(e\) and writes some value to the same address. Because if there is such a write operation, then \(RF\) will produce write operation \(e’\) instead of \(e\).
Take a previous example here:

These events are causally consistent because \(RF(rd(0,0,1)) = wr(0,0,1)\) and \(RF(rd(1,0,2)) = wr(1,0,2)\). Thus \(hb_{RF}(wr(0,0,1), rd(0,0,1))\) and \(hb _{RF}(wr(1,0,2), rd(1,0,2))\). We also know we can’t say \(hb _{SC}(wr(0,0,1), wr(1,0,2))\) because sequential consistency assumes no communication between processes. Therefore, \(hb _{RF}(wr(0,0,1), wr(1,0,2))\) doesn’t hold, and we can safely say these events are causally consistent.
Let’s look at another example:

This is because \(RF(rd(2,0,3)) = wr(0,0,3)\). However, there is a write operation \(wr(0,0,1)\) happening after \(wr(0,0,3)\) that write 1 to location 0. Therefore, it can’t be that \(wr(0,0,3)\) causes \(rd(2,0,3)\) because \(wr(0,0,1)\) interferes and creates a contradiction. The easiest way to detect whether a set of events is causally consistent is to see if there is a circle of dependencies.
S3 Strong Consistency
A consistency model widely used in production systems is the S3 consistency used in Amazon S3 storage service. The S3 consistency models holds:
- if \(hb(w_1, w_2)\) and \(hb(w_2, r)\), then \(RF(r) \neq w_1\)
- Two reads must agree on the order of writes that happen before both reads.
Here is an example that is causally consistent, but not S3 consistent:

The reason is \(rd(1,0,2)\) sees write options as \(wr(0,0,1) \rightarrow wr(1,0,2)\) and \(rd(0,0,1)\) sees \(wr(1,0,2)\rightarrow wr(0,0,1)\).
However, with slight adjustment to the example, we have S3 consistency.

The reason is because \(hb(wr(1,0,2),rd(0,0,2)\) doesn’t hold. So even if \(rd(1,0,2)\) sees write options as \(wr(0,0,1) \rightarrow wr(1,0,2)\) and \(rd(0,0,1)\) sees \(wr(1,0,2)\rightarrow wr(0,0,1)\), only \(wr(0,0,1)\) happens before both reads, thus they would agree on the ordering of writes.
Summary
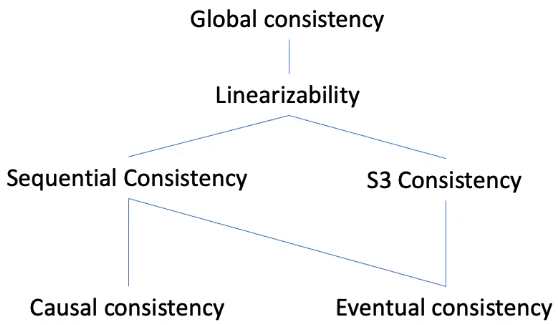
The consistency models discussed are only a tip of the iceberg. In fact, different storage service providers usually provide different consistency models. This may result in vendor lock-in because applications designed for one storage system may fall apart when deployed to another due to varying consistency implications.