Consensus Problem in Distributed Systems

In a distributed system, it is common for processes to reach consensus. When all non-faulty processes terminate, we must guarantee that everyone agrees on a specific value. Unfortunately, FLP 1985 ¹ proved that no asynchronous algorithms could achieve consensus.

Why is that an issue? The key lies in the fact that asynchronous communication doesn’t preserve order of message arrivals. To fully answer that question, we must introduce the concept of bi-valent state and \(v\)-valent state. The state of a system consists of possible states of all processes and all message queues. Bi-valent state means the system state can reach both decisions depending message arrival time; \(v\)-valent states indicates the system state can only reach one decision \(v\) (uni-valent).

Initial State Must be Bi-valent

We will use these facts to show why an algorithm will run infinitely under asynchronous assumptions. First, we claim that some initial state is bi-valent. This claim must be true by the proof of contradiction. Suppose we have some initial state that is uni-valent. We say two states are adjacent if all processes in both states agree on all values except one process. Two adjacent states must be either 0-valent or 1-valent (agree the global value is either 0 or 1).

For example, let’s say we have five processes in an initial uni-valent state (0-valent). We modify only one process’s value from 0 to 1 between two adjacent states. At some point in time, the system states changes from 0-valent to 1-valent (we refer to this moment as the crossover point).

We see at the crossover point the system state becomes 1-valent. Assume \(p_2\) fails before the crossover point, then according to adjacent states, some decision must be made, which contradicts with our assumption that all initial states are uni-valent. Therefore, we need the initial state to be bi-valent.

Always Bi-valent

Second, given the initial state is bi-valent, we then show that for any bi-valent state, we can always deliver the next message to process \(p\) while staying bi-valent. This means we can’t reach a certain decision no matter how much time has passed. More precisely, we will prove that no message can transform a system into a decided state by contradiction.

Suppose we have a system. Initially, this system state is 0-valent. We execute an event \(e = (p,m)\) (process \(p\) sends a message \(m\)). This event can either transform the system state \(C\) to 0-valent ot 1-valent at some point, while system state \(C\) can either be 0-valent or 1-valent.

At some point, the system state will change from \(C_0\) to \(C _1\). Let’s assume a different event \(e’ = (p’, m’)\) causes such transition of states. Now, we know previously that event \(e\) can transform the system to 0-valent or 1-valent. Now we have two situations: (1) \(e\) transforms \(C_0\) to 0-valent; (2) \(e\) transforms \(C _0\) to \(C _1\). We know \(e\) will tranform \(C _1\) to 1-valent. Therefore, we can also say after \(e\) is applied to \(C_0\) and leads to state 0-valent, we use apply \(e’\) to the system such that the system state becomes 1-valent. Therefore, if \(p \neq p’\), then \(e\) and \(e’\) commute. This will leads to contradiction.

To expand on this further, suppose event \(e\) leads to uni-valent state. Then, the absence of \(e\) (\(p\))-free will lead \(C _0\) to a decided state. In other words, \(p\)-free will lead the system to one decided states. However, we’ve shown \(e\) and \(e’\) commute, and now \(p\)-free, \(e\), and \(e’\) all commute, \(p\)-free will, in fact, leads the system to a ‘‘decided’’ state that is actually not decided, meaning we can’t reach a consensus. This scenario is shown below:

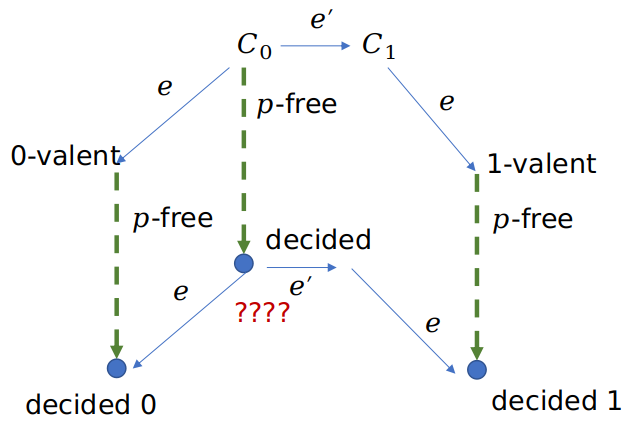
So, given the proof that we can’t reach consensus under asynchronous assumptions, what is the best we can do in practice?

Paxos Algorithm

We will back up a little bit from the asynchronous case, and make compromises by having: (1) consistency/agreement under the case of asynchrony; (2) settle for the lack of termination.

In Paxos algorithm, we assume the majority of process are non-faulty. That means \(N > 2F\). Processes have three roles: proposer, acceptor, and learner. Proposers broadcast its proposals to all acceptors; acceptors accept a proposal (e.g. based on arrival times of proposals) and broadcasts accept messages to all learners; learners decide which values to accept (e.g. the majority of a accepted value).

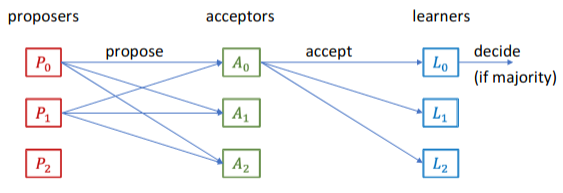
The problem is: even if one acceptor fails, the total number non-faulty processes will be \(N-1\) and we can’t say \(N-1 > 2F\) must hold.

To fix this problem, we can reduce the number proposers to one. At any moment, only one proposer is the leader. If a leader fails, a new leader becomes available and start sending out proposals.

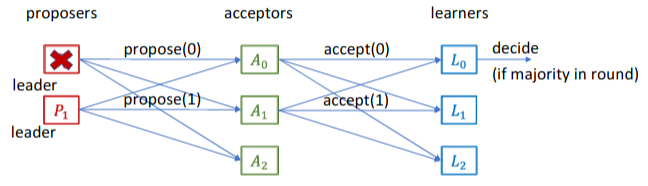
However, this solution still suffers from the same problem: if new leader is elected, it can not know whether the old leader’s proposal will be accepted.

Therefore, it is necessary for the new leader to establish a majority. The new leader must first broadcast a \(prepare\) message to all acceptors. Then acceptors will reply back with a \(prepared\) message back to the new leader. Therefore, when a majority is prepared, the new leader knows whether the old leader’s proposal might be accepted.

To see why this is the case, suppose an old leader dies at some point, then a new leader comes in. This new leader broadcasts a \(prepare\) message to acceptors. Some acceptors reply back. We argue that if the old leader’s proposal is accepted by the majority of acceptors, then this new leader will preserve the old proposal by evaluating the replies from acceptors and re-proposing the latest accepted value in the prepare phase.

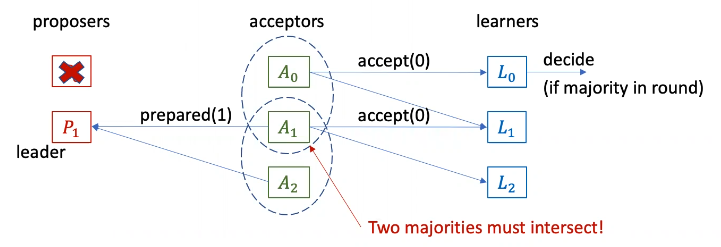
The reason is: if there exists a majority of acceptors in the previous round, then there must exist at least one acceptor in both the old and the current round, because add the sum of majorities exceeds the total number of processes. Therefore, there must be at least one acceptor that can send its accepted value back to the new leader. Since there is only one leader at any time, we can safely say the old value will be sent to the new leader.

In summary, if the new leader sees a prepare message with a value, then that value must come from the previous round and the new leader can re-propose that value; otherwise, the new leader can safely propose a new value.