Congruence Closure

This is a summary of how to compute congruence closure. I implemented the algorithm to compute congruence closure and thought I’d never forget it. But my memory starts to get blurry just after two days. So I figured I’d put things down so I don’t have to watch the entire lecture again the next time I need it.

Equivalence Relation

Equivalence relation has three properties: reflexive, symmetric, and transitive. (E.g. \(\geq\) is not an equivalence relation because it break the symmetric property. \(4 \geq 6\) does not imply that \(6 \geq 4\). For example, a binary relation $R$ over a set $S$ meeting these three properties can be expressed as:

• Reflexive: $\forall s \in S.\ sRs$
• Symmetric : $\forall s_1, s_2 \in S.\ s_1 R s_2 \rightarrow s_2 R s_1$
• Transitive: $\forall s_1, s_2, s_3 \in S.\ s_1 R s_2 \land s_2 R s_3 \rightarrow s_1 Rs_3$

Congruence Relation

Given a set $S$ equipped with functions $F = {f_1, …, f_n}$, a relation $R$ over $S$ is a congruence relation if $R$ is an equivalence relation and for every $n$‘ary function $f \in F$ we have:

\[\forall \overset{\rightarrow}{s}, \overset{\rightarrow}{t}.\ \bigwedge\limits_{i=1}^{n}s_i R t_i \rightarrow f(\overset{\rightarrow}{s}) R f(\overset{\rightarrow}{t})\]

A counter example would be given $R(x, y)$ defined as $|x| = |y|$ on all integers. If we have $R = {2, 2}$ and $f(x) = x + 1$ (successor function), then we know it violates the equivalence relation we mentioned above

Equivalence Closure

In short, the equivalence closure $R^E$ is the smallest equivalence relation that includes $R$. This is illustrated through an example. Given a set $S = {a, b, c}$ and binary relation $R:{\langle a, b \rangle , \langle b, c \rangle, \langle d, d \rangle}$, $R^E$ would contain all elements extended from $R$ based on the three properties of equivalence relation.

Congruence Closure

Naturally, congruence closure $R^C$ would be the smallest set that contains congruence relation $R$. What this means is $R^C$ contains $R^E$ (the equivlance closure we derived before), and any element generated from $R^E$ by a given function that produces element which also satisfies equivelance relation. For example, Given $S = {a, b, c}$ and function $f$ such that $f(a) = b$, $f(b) = c$, $f(c) = c$, the congruence closure would contain nine elments in total. First, we would use the procedure above to generated equivalence closure. Then, because $f(a) = b$ and $f(b) = c$ due to congruence relation, we know $b = c$, now we apply the procure for generating equivalence closure again.

Algorithm to Compute Congruence Closure

The high-level description of the algorithm is as following:

To decide satisfiability of $T_{=}$ (equality theory) formula:

\[F\ : \ s_1 = t_1 \land … s_m = t_m \land s_{m+1} \neq t_{m+1} \land … s_n \neq t_n\]

1. Compute subterms and construct initial DAG (each node’s representative is itself)
2. For each $i \in [1,m]$, process equality $s_i= t_i$ as described. (Essentially, process all equiv expression first)
3. For each $i \in [m + 1,n]$, check if $Rep(s_i) =Rep(t_i)$. (Check if any nequiv expression contradicts any equiv expression)
4. If there exists some $i \in [m + 1, n]$, for which $Rep(s_i) =Rep(t_i)$, return UNSAT
5. if for all $i$, $Rep(s_i) \neq Rep(t_i)$, return SAT

This is an example for illustration purposes, borrowed from Prof. Dillig’s slides:

Given formula $F\ : \ f^3(a) = a \land f^5(a) = a \land f(a) \neq a$

The initial DAG would be:

Process equality $f^3(a) = a$ gives us:

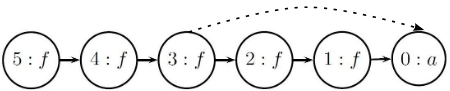
Recursively merging the parents results in:

Process equality $f^5(a) = a$ gives us:

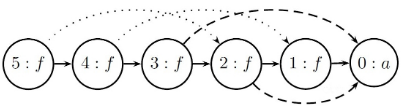
Now in this step, $f^2(a)$ and $a$ are in the same congruence class, thus we will perform the same operation on their parents, processing equality $f^3(a) = f(a)$:

We find $f(a) \neq a$ has a conflict because node $a$’s representative is $f(a)$, indicating they are in the same congruence class, meeting congruence relation. Thus the formula is UNSAT.